The formulas and their derivation are from
>function f(x,y) ...
th1=y[1]; th2=y[2]; dth=th1-th2; c=cos(th1-th2);
l=1; g=10; m=1; ml2=m*l^2;
pth1=y[3]; pth2=y[4];
Dth1=6/ml2*(2*pth1-3*c*pth2)/(16-9*c^2);
Dth2=6/ml2*(8*pth2-3*c*pth1)/(16-9*c^2);
return [Dth1,Dth2,
-ml2/2*(Dth1*Dth2*sin(th1-th2)+3*g/l*sin(th1)),
-ml2/2*(-Dth1*Dth2*sin(th1-th2)+g/l*sin(th2))]
endfunction
>t=0:0.01:50;
>s=ode("f",t,[0,0,4,4]); s=s[1:2]-pi/2;
The next plot shows all positions reached from the end of the second axis.
>plot2d(cos(s[1])+cos(s[2]),sin(s[1])+sin(s[2])):
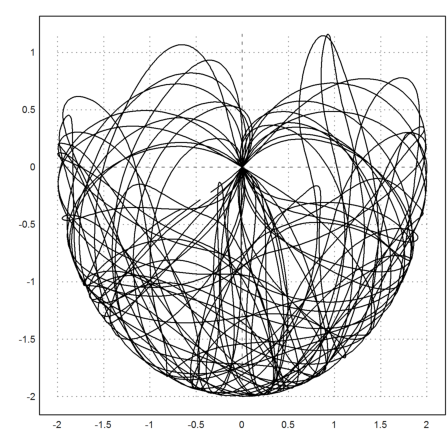
>t=0:0.05:50;
>s=ode("f",t,[0,0,4,4]); s=s[1:2]-pi/2;
We animate this.
>function anim (th1,th2) ...
setplot(-2,2,-2,2);
loop 1 to cols(th1)
clg;
a=th1[#]; b=th2[#];
lw=linewidth(3);
hold on;
plot([0,cos(a),(cos(a)+cos(b))],
[0,sin(a),(sin(a)+sin(b))]);
markerstyle("o#");
mark(0,0);
hold off;
linewidth(lw);
wait(0);
if testkey() then break; endif;
end;
endfunction
Press any key to sto the animation.
>anim(s[1],s[2]):
I have uploaded the animation to YouTube.